( الخاصية ab+c = ab + ac تسمى )
الخاصية ab+c = ab + ac تسمى
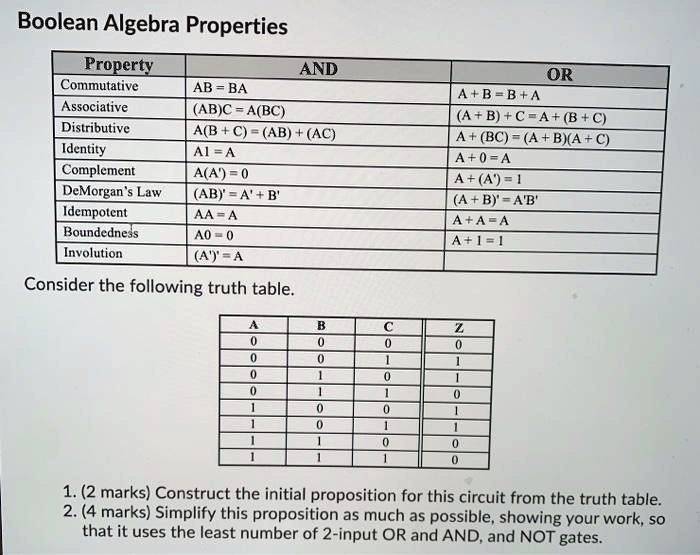
في الرياضيات، تُعرف الخاصية ab+c = ab + ac باسم الخاصية التوزيعية للأعداد الحقيقية. وتنص هذه الخاصية على أن ضرب مجموع عددين في عدد ثالث يساوي مجموع ناتج ضرب كل عدد من العددين في العدد الثالث.
أمثلة على الخاصية التوزيعية

دعنا نأخذ مثالًا بسيطًا لفهم الخاصية التوزيعية. لنفترض أن لدينا الأعداد الحقيقية a = 2، b = 3، و c = 4.
- ab + c = (2)(3) + 4 = 6 + 4 = 10
- ab + ac = (2)(3) + (2)(4) = 6 + 8 = 14

كما ترون، فإن ab + c = ab + ac، وهو ما يؤكد صحة الخاصية التوزيعية.

تطبيقات الخاصية التوزيعية
للخاصية التوزيعية تطبيقات عديدة في الرياضيات، بما في ذلك:

1. جمع وتبسيط التعبيرات الجبرية
- يمكن استخدام الخاصية التوزيعية لتجميع التعبيرات الجبرية وتبسيطها. على سبيل المثال:
- (2x + 3)(x + 4) = 2x(x + 4) + 3(x + 4) = 2x^2 + 8x + 3x + 12 = 2x^2 + 11x + 12

2. إيجاد مساحة المستطيلات
- يمكن استخدام الخاصية التوزيعية لإيجاد مساحة المستطيلات. على سبيل المثال، إذا كان طول المستطيل l وعرضه w، فإن مساحته هي:
- مساحة = طول × عرض = l × w = l(w + 0) = lw + 0 = lw
3. إيجاد حجم المكعبات
- يمكن استخدام الخاصية التوزيعية لإيجاد حجم المكعبات. على سبيل المثال، إذا كان طول ضلع المكعب هو s، فإن حجمه هو:
- حجم = طول × عرض × ارتفاع = s × s × s = s(s + 0) = s^2s + 0 = s^3

أنواع التوزيع
إلى جانب الخاصية التوزيعية للأعداد الحقيقية، هناك أنواع أخرى من التوزيع في الرياضيات، بما في ذلك:
1. التوزيع على الجمع
- تنص هذه الخاصية على أن ضرب مجموع عددين في عدد ثالث يساوي مجموع ناتج ضرب كل عدد من العددين في العدد الثالث:
- a(b + c) = ab + ac
2. التوزيع على الطرح
- تنص هذه الخاصية على أن ضرب طرح عددين في عدد ثالث يساوي طرح ناتج ضرب كل عدد من العددين في العدد الثالث:
- a(b – c) = ab – ac
3. التوزيع الخارجي
- تنص هذه الخاصية على أن ضرب عدد في مجموع حاصل قسمة عددين متساوي مع حاصل قسمة ضرب هذا العدد في كل عدد من هذين العددين:
- a(b / c) = (ab) / c
الخاصية التوزيعية للمصفوفات
تنطبق الخاصية التوزيعية أيضًا على المصفوفات. وتنص هذه الخاصية على أن ضرب مجموع مصفوفة في مصفوفة ثانية يساوي مجموع ناتج ضرب كل مصفوفة من المصفوفتين في المصفوفة الثانية:
A(B + C) = AB + AC
الخاصية التوزيعية للوحدات
تنطبق الخاصية التوزيعية أيضًا للوحدات. وتنص هذه الخاصية على أنه إذا كانت a و b و c كميات لها وحدات مختلفة، فإن ab + c لا معنى لها، ما لم يكن c = 0 أو a و b لهما نفس الوحدات.
الاستنتاج
الخاصية التوزيعية هي خاصية أساسية للأعداد الحقيقية والمصفوفات ولها تطبيقات عديدة في الرياضيات. وتساعد هذه الخاصية على جمع وتبسيط التعبيرات الجبرية، وإيجاد المساحات والأحجام، وفهم العلاقات بين العمليات الحسابية المختلفة.