( المكعب الذي يمكن الحصول عليه بثني المخطط هو…….. )

( المكعب الذي يمكن الحصول عليه بثني المخطط هو…….. )

المكعب: الشكل الهندسي ثلاثي الأبعاد

( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )

المكعب هو أحد الأشكال الهندسية ثلاثية الأبعاد التي تتميز بستة أوجه مربعة متساوية ومتعامدة مع بعضها البعض. كما يتميز المكعب باثني عشر ضلعًا وثماني رؤوس. يمكن الحصول على المكعب بثني مخطط ثنائي الأبعاد يسمى “شبكة المكعب” بطريقة معينة.

شبكة المكعب

شبكة المكعب هي مخطط ثنائي الأبعاد يُمثل جميع أوجه المكعب. تتكون الشبكة من ستة مربعات مفصولة بخطوط متعامدة تمثل حواف المكعب. لكل وجه من أوجه الشبكة رقم يمثل الرقم الموجود على الوجه المقابل للمكعب.
( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )

طريقة ثني شبكة المكعب

( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )

للحصول على مكعب من شبكته، يجب ثني الشبكة على طول الخطوط المتعامدة بحيث تتطابق الأرقام المتقابلة مع بعضها البعض. ثم يتم لصق أطراف المربعات معًا لتشكيل أوجه المكعب.

خصائص المكعب

له ستة أوجه مربعة متساوية.
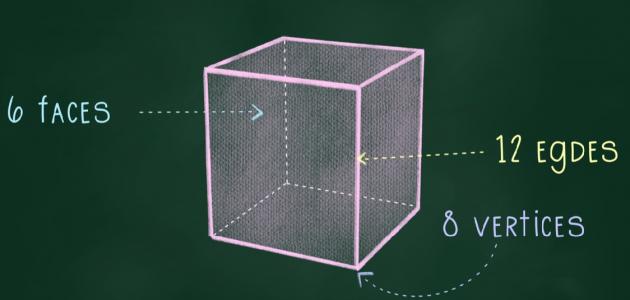
( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )
له اثنا عشر ضلعًا متساوية.
له ثماني رؤوس.
أقطاره متساوية ومتعامدة مع بعضها البعض.
جميع زواياه قائمة (90 درجة).

تطبيقات المكعب

يستخدم المكعب في العديد من التطبيقات اليومية مثل مكعبات الألعاب والزهر.
( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )
يستخدم أيضًا في الهندسة المعمارية والتصميم الصناعي.
( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )
يمكن استخدام المكعب كنموذج هندسي لتمثيل أشياء أو مفاهيم أخرى.

المكعب في الرياضيات

في الهندسة الرياضية، يعتبر المكعب من الأشكال الأولية التي تُدرس خصائصها وعلاقاتها بالأشكال الأخرى.
يستخدم المكعب في حساب الحجم والمساحة والمسافة.
( المكعب الذي يمكن الحصول عليه بثني المخطط هو........ )
يمكن استخدامه أيضًا في دراسة متعددات السطوح الأخرى.

المكعب في الطبيعة

يوجد المكعب في أشكال عديدة في الطبيعة مثل بلورات الملح والسكر.
يمكن رؤية مكعبات صغيرة في بنية بعض المواد مثل الرغوة والإسفنج.
يمكن العثور على أشكال تشبه المكعب في أشياء مثل خلايا النحل والتراكيب البلورية.

خاتمة

المكعب هو شكل هندسي متعدد الاستخدامات له خصائص وصفات فريدة تجعله مفيدًا في مجموعة واسعة من التطبيقات. من بنائه من شبكة ثنائية الأبعاد إلى تطبيقاته في الرياضيات والعلوم والطبيعة، يعتبر المكعب من الأشكال المهمة التي لها دور بارز في فهم عالمنا.

شاهد ايضا:

  1. ( ماهو تعريف بروتوكول الشبكة )
  2. ( برنامج أو جهاز يستخدم لأمان الشبكة ويعتمد على التحكم في حركة نقل البيانات الواردة والصادرة من خلال تحليل حزم البيانات وتحديد ما إذا كان ين
  3. ( مصطلح يشير إلى مجموعة من البروتوكولات وبرامج الأدوات المساعدة التي تدعم اتصال الشبكة منخفضة المستوى )
  4. ( مجموعة القوانين التي تحدد كيف يتم تنسيق ومعالجة البيانات التي تمر عبر الشبكة )
  5. ( نفخة الصور تكون يوم )
  6. ( لهم البشرى في الحياة الدنيا ) ما هذه البشرى
  7. ( الشبكة العنكبوتية العالمية تعد أحد أهم خدمات الانترنت صح أم خطأ )
  8. ( غَابَةُ رَغَدَانِ مِنَ الْغَابَاتِ فِي مَنْطِقَةِ الْبَاحَةِ )
  9. اختر عبارتين متكافئتين تمثلان مساحة الشكل أدناه
  10. ( ماهو تعريف الشبكه العنكبوتيه )

أضف تعليق